「有界な単調数列は収束する」の証明
『経済学のための数学入門』、定理2.2.2(71頁)。
有界な単調数列は収束する。
単調増加なら最小上界が、単調減少なら最大下界が、収束先である。
有界(とか上界とか下界)についてはまずこちら。あとこちらも。
それから、実数列の収束についてはこちら。
有界かどうかというのはとりあえず集合の話ですが、実数列は集合ではないので、まずは「実数列が有界である」とはどういうことかを定義しましょう。
実数列
実数を要素とする集合において、上に有界というのは、その集合のどの要素よりも大きな(小さくない)実数(=上界)が外にある、ということであり、また下に有界というのは、どの要素よりも小さな(大きくない)実数(下界)が外にある、ということですね。
最小上界というのは、上界の中で最小のもの、つまりそれより小さい上界が存在しないような上界のことであり、最大下界とは、下界の中で最大のもの、つまりそれより大きい下界が存在しないような下界のことです。
単調というのは、実数列の要素が、順番を追うごとにに必ず大きくなっていく(途中で前のより小さくならない)とか、順番を追うごとに小さくなっていく(途中で前のより大きくならない)、といったことです。前者が単調増加、後者が単調減少です。
単調増加:
単調減少: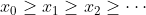
証明は結構簡単です。
定理の仮定ですので、
とします。 は
の上界ですから、
ですね。それから、 を任意に導入しますと、
は
より小さいので、これは上界ではありえません(だって
が最小上界なんだもん)。
ということは、 の要素の中に、
となるような が存在するということです。単調増加ですから、
が成り立ちます。上の結果とあわせると、
ですね。これをちょっと移項して変形すると、
となりますが、ということは
となります。これはまさに、 が、
に収束するということですね。「単調増加で上に有界なら最小上界に収束する」の証明はこれで終わりです。
「単調減少で下に有界なら最大下界に収束する」の方も、証明の形式は基本的に同じなので、こっちは簡単にささっと書いておきます。
定理2.1.1により、下に有界なら最大下界が存在するので、それを
とします。これが最大下界なので は下界ではありえません。ということは、単調減少なので、どっかの要素
以降はそれより小さいということです。つまり
ですね。これを変形すると
となって、つまり
となって、これはまさに、 が、
に収束する、ということですね。これで証明は終わりです。