前回、連立方程式
 \left( \begin{matrix} x \\ y \end{matrix} \right) = \left( \begin{matrix} e \\ f \end{matrix} \right)})
の解が

となることをやったよ。今回は、なんでそうなるのかだよ。
とりあえず
})
と書くことにするよ。最初の連立方程式は
 = \left( \begin{matrix} e \\ f \end{matrix} \right)})
と書けるよ。ここで 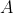 の逆行列を
の逆行列を 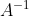 と書くことにするよ。逆行列というのは元の行列にかけると単位行列になるような行列だよ(普通の数に逆数をかけると
と書くことにするよ。逆行列というのは元の行列にかけると単位行列になるような行列だよ(普通の数に逆数をかけると 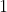 になるのと同じだよ。)。
になるのと同じだよ。)。
最初の連立方程式の両辺に左から 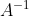 をかけてみるよ。
をかけてみるよ。
 = A^{-1} \left( \begin{matrix} e \\ f \end{matrix} \right)})
すると
 = A^{-1} \left( \begin{matrix} e \\ f \end{matrix} \right)})
となって、右辺を計算すれば解が出ることがわかるよ。ここで、一般に逆行列というのは
})
となっているよ(元の行列の行列式の逆数が前に出て、行列の中は(1)  と
と 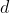 を交換、(2)
を交換、(2) 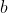 と
と  の符号を逆転)。なので、
の符号を逆転)。なので、
 = \frac{1}{\left| A \right|} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) \left( \begin{matrix} e \\ f \end{matrix} \right) = \frac{1}{\left| A \right|} \left( \begin{matrix} ed-bf \\ af-ec \end{matrix} \right)})
となるよ。

だから、これで、行列式を使った解き方と逆行列をかける解き方が結局同じこと(前者は後者の簡単版)であることがわかったよ。